Yue Wu’s Research Page
Research Interests
- High-order numerical methods for PDEs:
- Finite element methods
- Discontinuous Galerkin methods
- Spectral methods
- Finite difference / volume methods
- Scientific computing:
- Parallel numerical solvers
- Iterative methods
Research Experiences
1. Numerical Simulation of Plasma Equilibrium Evolution in Nuclear Fusion
Undergraduate Research Program at USTC
Supervisor: Prof. Mengping ZHANG
07/2021 ~ 05/2022, USTC
Defense: 12/30/2022
The controlled nuclear fusion is one of the most prospective solution to the energy crisis and environmental problems. The tokamak has been widely investigated as the most feasible magnetically confined fusion device. Tearing mode instabilities have great influence on the fusion reaction thus worth studying.
In this research, in order to simulate the evolution process of tokamak plasma instability numerically, we reviewed different formulations of the MHD equations, selected a suitable type of non-conservative resistive MHD, and developed a parallel solver using hybrid finite difference-Fourier pseudo spectral method in cylindrical coordinates. Using our solver, we simulated the (m,n)=(2,1) resistive tearing mode instability, and checked the results against those obtained from the CLT and M3D-C1 code with researchers from Institute of Plasma Physics, Chinese Academy of Science. Our solver exhibits satisfactory performance in conserving numerical divergence of the magnetic field, fitting the theoretical relation between logarithmic growth rate of kinetic energy and resistivity, revealing the tearing mode structure independent of initial perturbation at the linear stage, and reaching the final saturation stage.
Below is a plot of the perturbation on the toroidal component of the electric field at time T=7000, which reveals the resistive tearing mode structure and should be independent of the initial perturbation, and a log-plot of kinetic energy evolution under different resistivity. Our code reveals the linear growing stage, mode structure and the logarithmic growth rate very well.
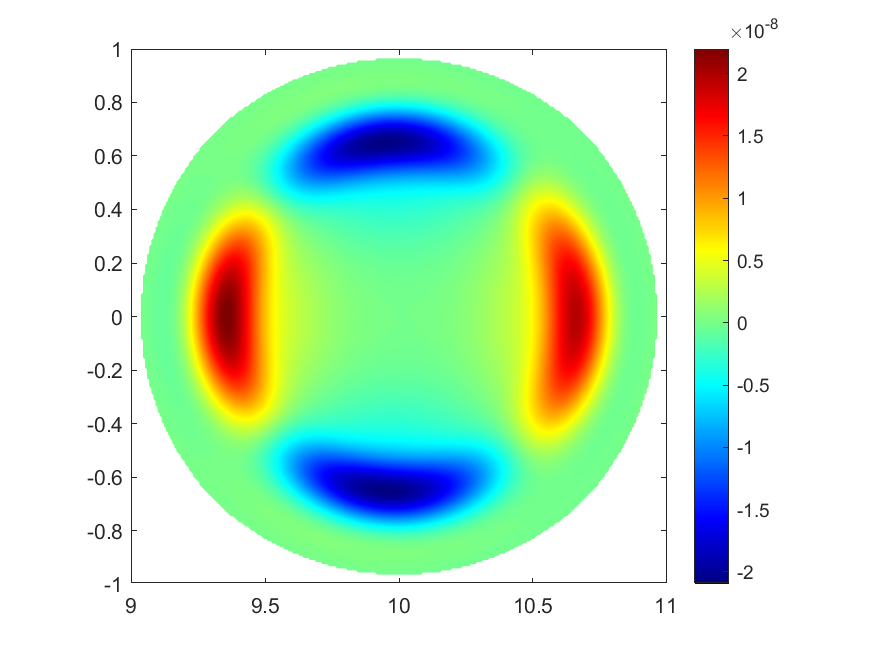
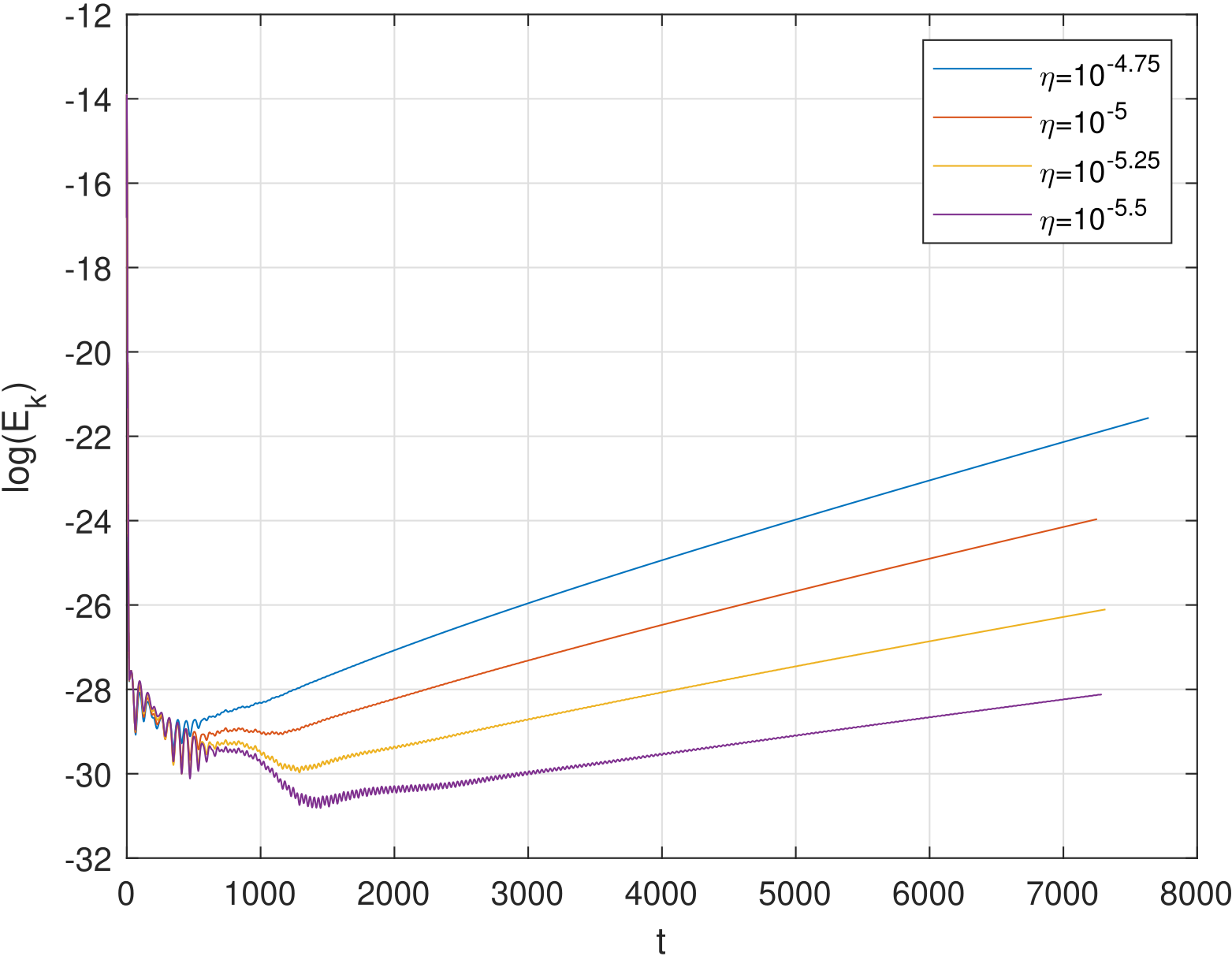
We virtually discussed this research with Prof. Chi-Wang SHU. Thanks for his discussion and advice.
Research report (in Chinese) preview: here; Defense PPT (in Chinese) preview: here.
2. Positivity-Preserving Conservative Low-Rank Methods for Vlasov Dynamics
Supervisor: Prof. Xiangxiong ZHANG
06/2022 ~ 08/2022, Purdue University (remote)
The high-dimensionality of Vlasov dynamics makes it expensive to solve by traditional numerical methods. Utilizing the low-rank structure of the solution, people have developed cost-efficient methods using low-rank matrix/tensor approximation. However, very often a low-rank approximation of a given non-negative matrix (which corresponds to the solution) can have negative elements which results in non-physical solutions. In this research, our goal is to develop a cost-efficient positivity-preserving conservative low-rank method to solve this problem. We designed two algorithms, one is the tangent-space accelerated alternating projection algorithm, and the other is the nuclear norm optimization, both with macroscopic quantities conservation.
We virtually discussed this research with Prof. Jing-Mei QIU. Thanks for her discussion and data.
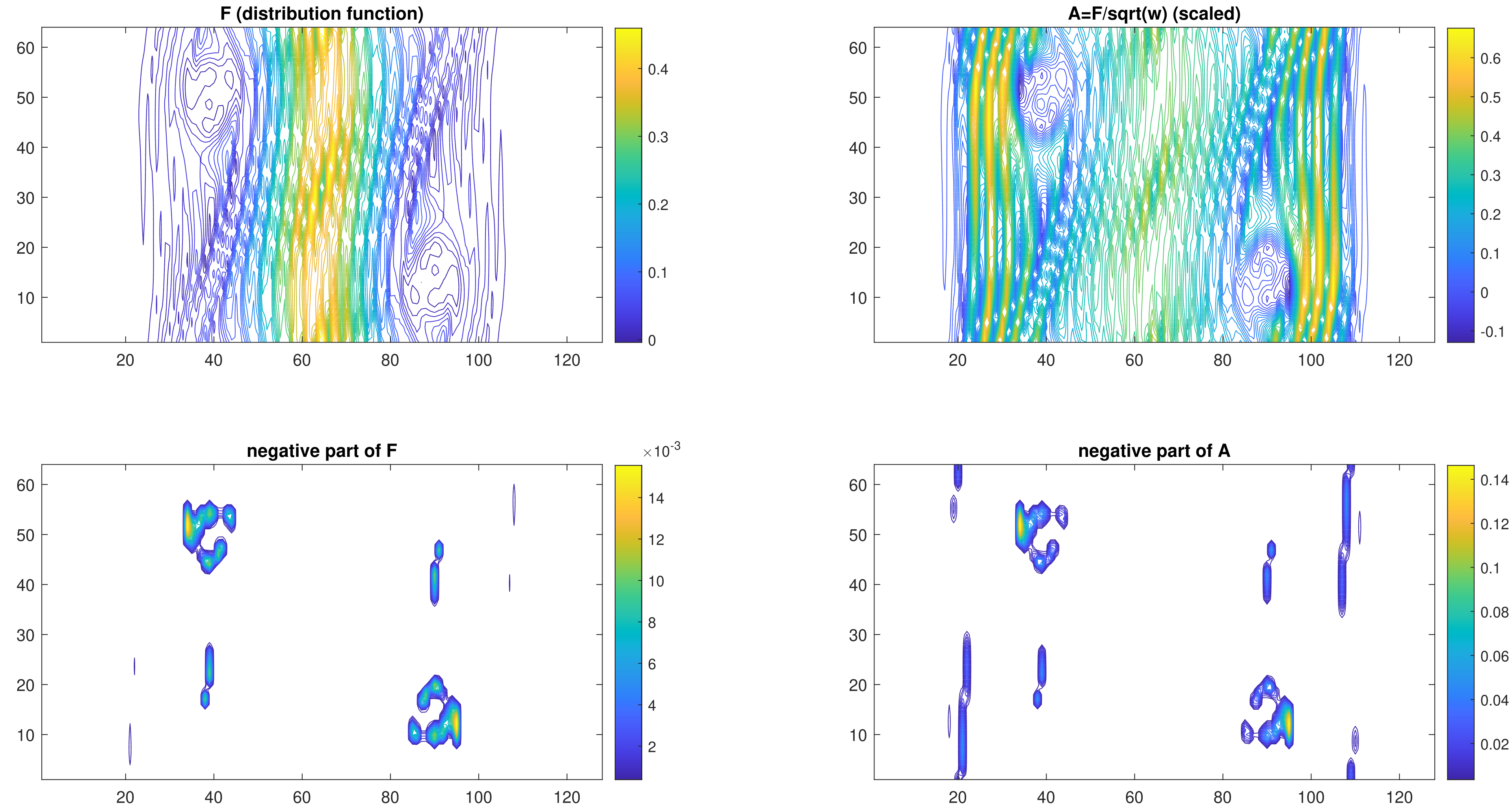
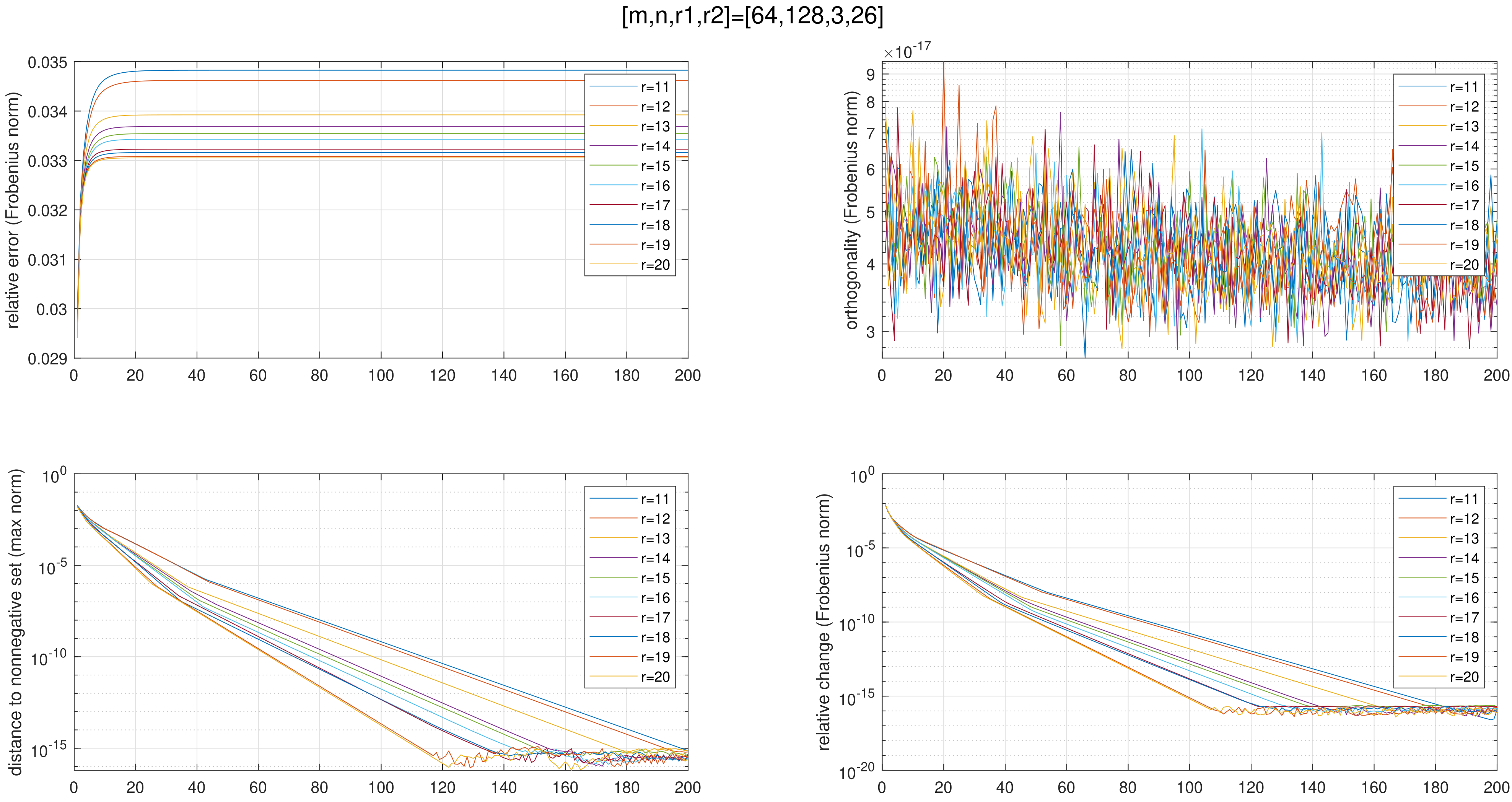
3. Discontinuous Galerkin Methods for the p-Laplace Equation
Bachelor’s Thesis at USTC
Supervisor: Prof. Yan XU
12/2022 ~ 06/2023, USTC
Defense: 06/07/2023
We study the high-order local discontinuous Galerkin (LDG) method for the p-Laplace equation. We reformulate our spatial discretization as an equivalent convex minimization problem and use a preconditioned gradient descent method as the nonlinear solver. For the first time, a weighted preconditioner that provides hk-independent convergence is applied in the LDG setting. For polynomial order k ≥ 1, we rigorously establish the solvability of our scheme and provide a priori error estimates in a mesh-dependent energy norm. Our error estimates are under a different and non-equivalent distance from existing LDG results. For arbitrarily high-order polynomials under the assumption that the exact solution has enough regularity, the error estimates demonstrate the potential for high-order accuracy. Our numerical results exhibit the desired convergence speed facilitated by the preconditioner, and we observe best convergence rates in gradient variables in alignment with linear LDG, and optimal rates in the primal variable when 1 < p ≤ 2.
arXiv preprint (submitted): here
Numerical PDE Programming (choronological order)
| PDE | method | domain | mesh | language |
|---|---|---|---|---|
| Poisson (Dirichlet) | 2-order FD | 2D rectangle | uniform Cartesian | Matlab |
| compressible Euler | 5-order FD-WENO | 1D interval | uniform Cartesian | Fortran |
| compressible Navier–Stokes | 5-order FD-WENO | 2D rectangle | uniform Cartesian | Fortran + OpenMP |
| Hamilton-Jacobi | 5-order FD-WENO | 2D rectangle | uniform Cartesian | Fortran + OpenMP |
| compressible RMHD | 5-order FD-HJ | 2D rectangle | uniform Cartesian | Fortran + OpenMP |
| compressible RMHD | 4-order FD-HJ + Fourier | 3D toroidal with rectangular section | uniform Cylindrical | Fortran + OpenMP |
| compressible RMHD | 3-order FD-HJ + Fourier | 3D toroidal with circular section | uniform Cartesian (embedded) | Fortran + OpenMP + MPI |
| compressible MHD | arbitrary-degree DG (locally div-free) | 2D rectangle | arbitrary Cartesian | Fortran + OpenMP + MPI |
| Poisson | arbitrary-degree FEM | 1D interval | arbitrary Cartesian | Matlab |
| Poisson | quadratic FEM | 2D polygon | triangular | Matlab |
| Poisson | LDG | 1D interval | arbitrary Cartesian | Matlab |
| Poisson | HDG | 1D interval | arbitrary Cartesian | Matlab |
| Poisson | arbitrary-degree MD-LDG (good results up to k=9) | 2D polygon | triangular | Matlab |
| p-Laplace | arbitrary-degree LDG | 1D interval | arbitrary Cartesian | Matlab |
| p-Laplace | arbitrary-degree LDG | 2D polygon | triangular | Matlab |
| mixed FEM | arbitrary-degree FEM | 2D polygon | triangular | MFEM |
